Einführung in die Welt der Daten
Daten sind heute der Treibstoff der digitalen Welt. Ob beim Online-Shopping, bei der Navigation mit Google Maps oder beim Streamen auf Spotify - überall werden Daten erzeugt, übertragen und analysiert. Unternehmen treffen auf Basis von Daten Entscheidungen, Maschinen reagieren auf Messwerte, und selbst unser Smartphone lernt aus unseren Gewohnheiten.
Ohne Daten würde vieles, was für uns selbstverständlich ist, schlicht nicht funktionieren. Doch um zu verstehen, warum Daten so zentral sind, müssen wir uns zunächst ansehen, was Daten eigentlich sind - und wie sie sich von Information und Wissen unterscheiden.
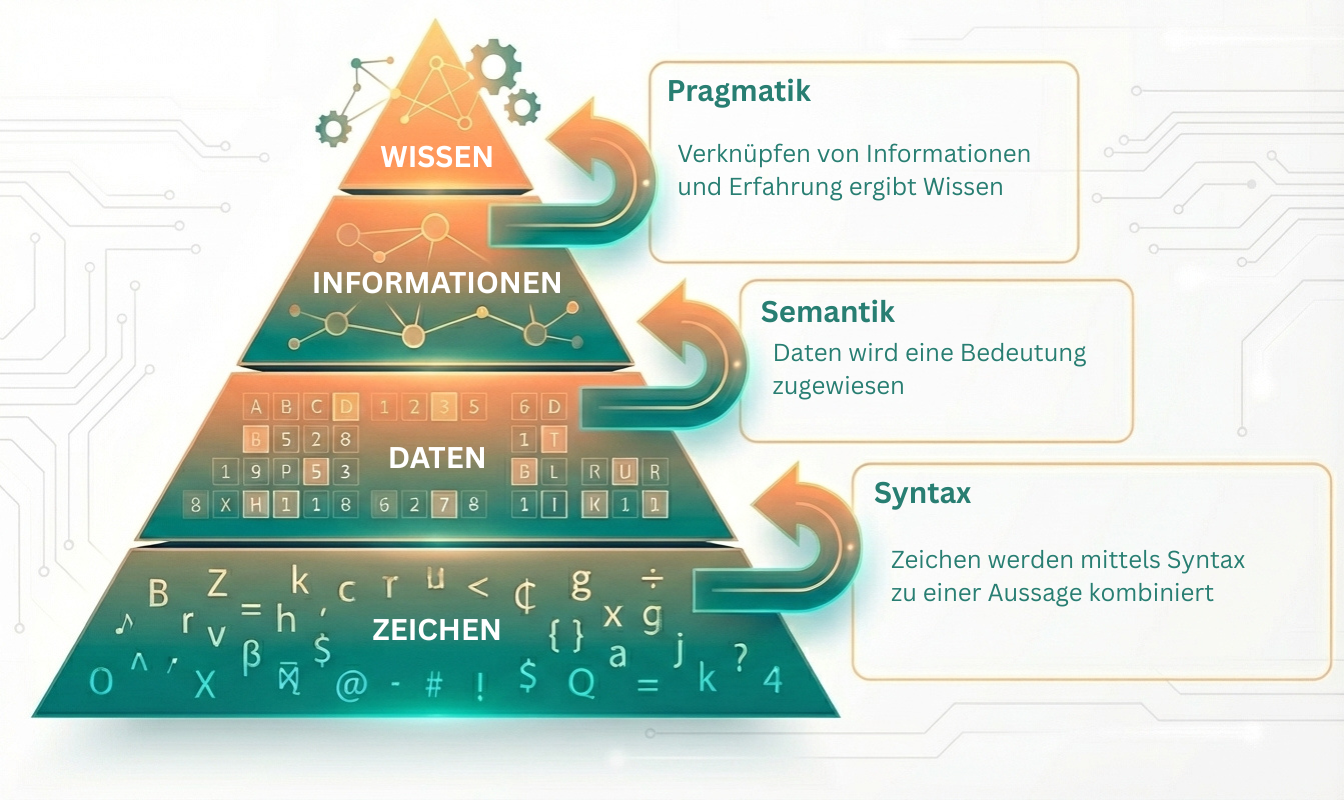
Von Daten zum Wissen 🧠
Daten sind zunächst einmal Rohmaterial - einzelne, isolierte Fakten, die für sich genommen keine Bedeutung tragen. Erst wenn wir sie in einen Kontext setzen (Semantik), entstehen Informationen. Und wenn wir diese Informationen anwenden und verknüpfen (Pragmatik), also Entscheidungen daraus ableiten, sprechen wir von Wissen.
Dieses Prinzip begegnet uns täglich: In einer Fitness-App werden Schritte gezählt (Daten), daraus wird der Kalorienverbrauch berechnet (Information) - und das Wissen daraus motiviert uns, unser Tagesziel zu erreichen (Wissen).
Damit wird klar: Daten sind nicht Selbstzweck, sondern der Ausgangspunkt eines Verarbeitungsprozesses, der von der Erfassung bis zur Anwendung reicht.

Reflexionsfrage
Überlege dir ein Beispiel aus deinem Alltag, bei dem du unbewusst Daten in Information oder Wissen verwandelst.
Wie können Daten unterschieden werden?
Bevor wir Daten analysieren oder Modelle darauf anwenden, müssen wir sie verstehen. Das bedeutet: Wir müssen wissen, welche Eigenschaften die Daten haben, welche Strukturen sie aufweisen und welche Probleme sie mitbringen.
Denn reale Daten sind selten „sauber“:
- Sensordaten enthalten oft fehlende Werte oder Messfehler,
- Social-Media-Daten sind unstrukturiert (Text, Bild, Video),
- Finanzdaten enthalten Ausreißer oder extreme Werte, die Analysen verzerren können.
Ein gutes Verständnis der Daten ist deshalb die Grundlage jeder erfolgreichen Datenvorverarbeitung – also der Phase, in der Daten aufbereitet, bereinigt und in ein nutzbares Format gebracht werden. Nur wer seine Daten kennt, kann sie richtig interpretieren und nutzen. In weiterer Folge betrachten wir unterschiedliche Möglichkeiten, Daten zu klassifizieren und charakterisieren.
Klassische Daten vs. Big Data
Wenn wir von "Daten" sprechen, denken viele zunächst an Tabellen mit Zahlen und Texten - klassische Daten, wie sie in Excel oder relationalen Datenbanken gespeichert sind. Diese Daten sind meist strukturiert, leicht zu durchsuchen und stammen aus klar definierten Quellen (z. B. Kundendaten, Rechnungen, Lagerbestände).
Mit dem digitalen Wandel kamen jedoch neue Formen der Datenerzeugung hinzu: Sensoren, Smartphones, soziale Netzwerke, Kameras, Maschinen. Dadurch entstanden riesige, heterogene Datenmengen - das Zeitalter der Big Data.
Big Data wird oft durch die 3 V beschrieben:
- Volume - die Menge: Daten in großem Ausmaß vor (Terabyte- oder Petabyte-Bereich).
- Velocity - die Geschwindigkeit: Daten entstehen in enormer Geschwindigkeit, z. B. bei Börsenkursen oder in Industrieanlagen.
- Variety - die Vielfalt: Texte, Bilder, Videos, Audiosignale, Sensordaten u.v.m. sollen verarbeitet werden.
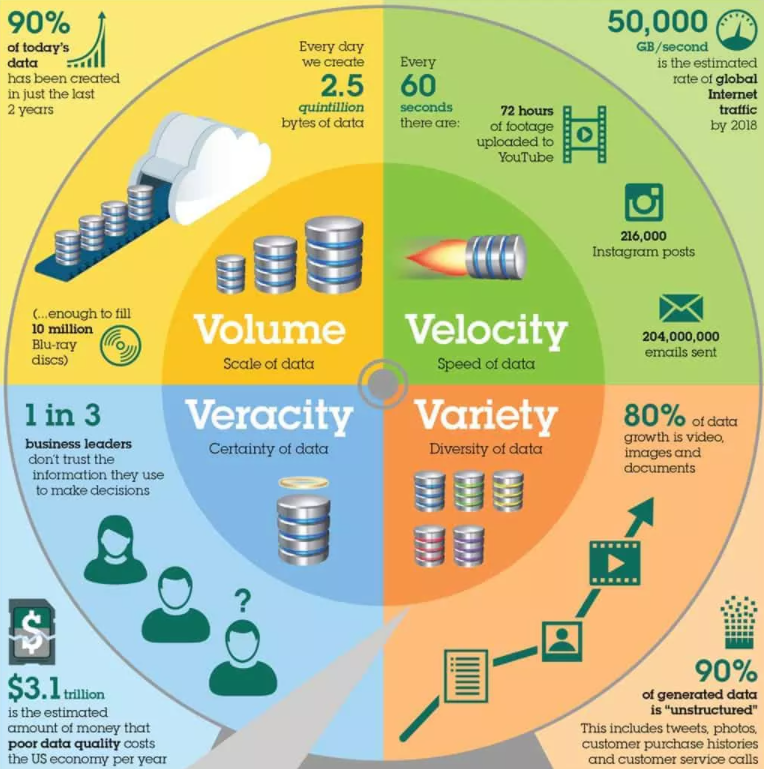

Diese Vielfalt bringt Chancen, aber auch neue Herausforderungen. Während klassische Datenbanken gut geeignet sind, strukturierte Informationen zu speichern, müssen Big-Data-Systeme unstrukturierte Daten verarbeiten, Verknüpfungen herstellen und Muster erkennen - oft mithilfe von künstlicher Intelligenz.
Beispiel: Klassische & Big Data
Ein Online-Shop speichert seine Bestellungen (klassische Daten) in einer Datenbank. Zusätzlich analysiert er Social-Media-Beiträge, Wetterdaten und Standortinformationen (Big Data), um vorherzusagen, welche Produkte morgen besonders gefragt sein werden.
Damit verschiebt sich der Fokus: Weg vom reinen Speichern - hin zum Verstehen und Nutzen der Daten.
Big Data
Überlege drei Situationen, in denen Unternehmen Big Data nutzen könnten. Schreibe zu jedem Beispiel kurz dazu, welche der drei „V“-Eigenschaften (Volume, Velocity, Variety) besonders relevant ist.

Datenarten
Ein weiteres Unterscheidungsmerkmal ist die Datenart. Um Daten sinnvoll zu verwalten, ist es hilfreich, ihre Form und Herkunft zu verstehen. Denn je nach Art benötigen sie unterschiedliche Speicher- und Analyseverfahren.
Beispiel: Mischform
In der Praxis treten oft Mischformen auf:
Ein modernes Auto erzeugt Bilddaten (Kameras), Sensordaten (Radar, Lidar) und Textdaten (Fehlerprotokolle) – gleichzeitig und in Echtzeit.
Dieser technologische Mix zeigt, dass der Begriff "Daten" weit über Tabellen hinausgeht: Alles, was sich digital erfassen und speichern lässt, sind Daten.
Qualitative vs. Quantitative Daten
Daten unterscheiden sich nicht nur im Inhalt, sondern auch in der Art der Darstellung.
Qualitative (kategorische) Daten
Eine Variable wird als qualitativ (kategorial) bezeichnet, wenn jede Beobachtung eindeutig einer bestimmten Kategorie zugeordnet werden kann. Qualitative Variablen drücken unterschiedliche Eigenschaften oder Merkmale aus, ohne eine Größe oder ein Ausmaß anzugeben.
Beispiel: Qualitative Daten
- Geschlecht (m/w/d)
- Augenfarbe (blau, braun, grün)
- Nationalität (AT, DE, IT)
Quantitative (numerische) Daten
Dem gegenüber wird eine Variable als quantitativ (numerisch) bezeichnet, wenn sie das Ausmaß oder die Größe einer Eigenschaft misst. Quantitative Variablen können in zwei Typen unterteilt werden:
- Diskrete Variablen: Die Variable kann nur eine endliche oder abzählbare Anzahl von Werten annehmen.
- Kontinuierliche Variablen: Die Variable kann jeden Wert innerhalb eines bestimmten Intervalls annehmen.
Beispiel: Qualitativ vs. Quantitativ
- Qualitativ: Religion, Geschlecht, Wohnort
- Quantitativ – diskret: Anzahl der Bestellungen, Stückzahl
- Quantitativ – stetig: Umsatz in €, Temperatur, Körpergröße
Hinweis
Nicht alle Zahlen sind automatisch quantitativ! Nur weil etwas mit Zahlen dargestellt wird, heißt das nicht automatisch, dass es eine numerische (messbare) Eigenschaft beschreibt.
Beispiel: Eine Trikotnummer im Sport (z. B. Spieler Nummer 10) ist keine messbare Zahl. Die "10" steht hier nur als Bezeichner für eine Person, nicht für eine messbare Eigenschaft wie Länge, Gewicht oder Alter.
Das heißt: Eine Zahl ist nur dann quantitativ, wenn sie ein Messwert ist – also ein Ausmaß einer Eigenschaft ausdrückt (z. B. Gewicht, Preis, Alter). Wenn sie dagegen nur zur Unterscheidung oder Kennzeichnung dient, ist sie qualitativ.
Qualitative und Quantiative Daten
Nenne zu jedem der folgenden Begriffe, ob er qualitativ oder quantitativ ist:
- Postleitzahl
- Körpergröße
- Note
- Blutgruppe
Attributtypen
Nachdem wir qualitative und quantitative Daten unterschieden haben, betrachten wir nun feinere Abstufungen, sogenannte Skalenniveaus. Diese bestimmen, welche mathematischen Operationen erlaubt sind - z. B. ob man Mittelwerte bilden darf oder nur vergleichen kann.
Um Daten zu strukturieren, werden sie in Attribute zerlegt - also Merkmale, die ein Objekt oder Ereignis beschreiben.
Beispiel: Attribute
Für das Objekt Student könnten die Attribute Name, Matrikelnummer, Studiengang und Geburtsdatum definiert werden.
Nicht jedes Attribut ist gleichartig. In der Statistik und Datenanalyse unterscheidet man verschiedene Skalenniveaus: kategorial (nominal oder ordinal) und metrisch/numerisch (intervallskaliert oder verhältnisskaliert).
Die richtige Zuordnung ist entscheidend, da sie bestimmt, welche Analysen zulässig sind: Mit Nominaldaten kann man zählen, mit Ordinaldaten sortieren und mit Verhältnisskalen rechnen. Wer also Daten richtig verstehen will, muss wissen, welches Skalenniveo sie haben.
Nominale Attribute
Nominale Attribute sind Kategorien ohne natürliche Reihenfolge. Sie bestehen aus Namen, Symbolen oder Codes, die Gruppen kennzeichnen.
Beispiel: Nominal
- Automarken: BMW, Audi, VW, Skoda, Tesla
- Haarfarbe: blond, braun, schwarz
- Beruf: Lehrer, Arzt, Programmierer
Anhand dieser Beispiele erkennt man, dass es möglich ist zu überprüfen, ob zwei Werte gleich oder ungleich sind, aber nicht, ob einer größer ist.
Hinweis
Nominale Attribute können auch als Zahlen codiert werden – diese Zahlen haben aber keine rechnerische Bedeutung.
Beispiel Automarken: Wir könnten für jede Automarke eine eindeutige Nummer vergeben und unsere Daten damit codieren. Dann wäre beispielsweise BMW = 1, Audi = 2, VW = 3 usw. Mathematisch könnte ich nun sagen dass 2 (Audi) größer ist als 1 (BMW). Da die inhaltliche Bedeutung der Daten aber nicht verändert wurde, ist diese Aussage weiterhin nicht sinnvoll.
Dies bedeutet nun in weiterer Folge, dass die Berechnung des arithmetischen Mittelwerts oder des Medians entweder nicht möglich oder nicht sinnvoll ist. Einzig die Berechnung des Modus (häufigster Wert) führt zu einer matematisch und logisch sinnvollen Aussage.
Ein Sonderfall von nominalen Attributen sind Binäre Attribute welche nur zwei Kategorien besitzen.
Diese Kategorien werden häufig durch die Zahlen 0 und 1* dargestellt, wobei 0 das Fehlen und 1 das vorhandensein des Merkmals kennzeichnet. Diese binäre Klassifikation wird in der Datenanalyse häufig verwendet, um einfache Variablen darzustellen.
Beispiel: Nominal-Binär
- Raucher: Ja = 1, Nein = 0
- Test positiv = 1, negativ = 0
Ordinale Attribute
Auf der nächsten Stufe der Skalenniveaus befinden sich Ordinale Attribute. Diese haben eine natürliche Reihenfolge, aber die Abstände zwischen den Stufen sind nicht messbar.
Beispiel: Ordinal
- Getränkegrößen (klein, mittel groß)
- Zufriedenheitsbewertungen (hoch, mittel, niedrig)
- T-Shirt-Größen (S, M, L, XL)
Bei den gezeigten Beispielen erkennt man, dass eine Aussage wie "etwas ist größer/schneller/besser als" zulässig ist, wenngleich man aber nicht weiß, wie viel größer. Dies bedeutet, dass Vergleiche ("besser als", "kleiner als") erlaubt sind, aber keine Differenz- oder Durchschnittsberechnungen.
Daher ist es möglich und sinnvoll, den Median und den Modus zu berechnen. Der (arithmetische) Mittelwert hingegen ist nicht sinnvoll.
Intervallskalierte Attribute
Intervallskalierte Attribute können auf einer Skala mit gleich großen Einheiten gemessen werden, wodurch konstante und vergleichbare Abstände zwischen den Werten möglich sind. Diese Attribute besitzen eine natürliche Reihenfolge und können positive, null oder negative Werte annehmen.
Das bedeutet, dass eine Rangordnung der Werte sowohl möglich als auch sinnvoll ist und ein klares Gefühl von Zunahme oder Abnahme entlang der Skala vermittelt. Einzig der Nullpunkt ist willkürlich gewählt.
Beispiel: Intervallskaliert
- Temperatur in °C (0°C ist nicht „keine Temperatur“)
- Kalenderjahre (das Jahr 0 ist willkürlich gewählt)
Wie bei der Ordinalskala kann man auch bei der Intervallskala feststellen, ob zwei Werte gleich sind und ob ein Wert höher ist als eine andere. Zusätzlich lässt sich der Unterschied zwischen Werten sinnvoll interpretieren.
Da jedoch der Nullpunkt willkürlich festgelegt ist (z. B. 0°C = Gefrierpunkt von Wasser), können Verhältnisse (Quotienten) nicht sinnvoll interpretiert werden. So ist es z. B. nicht korrekt zu sagen, dass 20°C "doppelt so warm" ist wie 10°C.
Sowohl für intervallskalierte Attribute als auch für die nachfolgenden verhältnisskalierten Attribute können sowohl Modus, Median als auch das arithmetische Mittel berechnet und sinnvoll interpretiert werden.
Verhältnisskalierte Attribute
Verhältnisskalierte Attribute besitzen einen natürlichen Nullpunkt, der das vollständige Fehlen des Merkmals anzeigt. Diese Eigenschaft ermöglicht es, einen Wert als ein Vielfaches eines anderen sinnvoll zu interpretieren.
Dadurch erlauben verhältnisskalierte Daten eine große Bandbreite mathematischer Operationen, einschließlich aussagekräftiger Vergleiche sowohl von Unterschieden als auch von Verhältnissen zwischen den Werten.
Beispiel: Verhältnisskaliert
- Temperatur in Kelvin
- Alter, Einkommen, Gewicht, Entfernung
Die Verhältnisskala ist das höhchste Skalenniveau in der Statistik und erlaubt alle mathematischen Operationen: Mittelwert, Median, Varianz, Verhältnisvergleiche usw.
Skalenniveaus
Je höher das Skalenniveau, desto mehr Rechenoperationen sind erlaubt. Nominal → Ordinal → Intervall → Verhältnis
Übungsaufgabe: Attributtypen bestimmen
Bestimme für die folgenden Attribute den Skalenniveau-Typ und begründe deine Entscheidung:
- Alter
- Beruf
- Schulnote
- Temperatur in °C
- Entfernung in Metern
Von der Theorie zur Praxis
Bislang haben wir Daten auf semantischer Ebene betrachtet – ihre Bedeutung, Struktur und Klassifikation. Wir wissen jetzt, was Daten sind, wie sie sich unterscheiden lassen und welche Rolle sie in der digitalen Welt spielen.
Doch eine zentrale Frage haben wir noch nicht beantwortet: Wie entstehen Daten überhaupt?
Wenn wir von „Temperatur: 23,5°C" oder „Geschwindigkeit: 87 km/h" sprechen, dann wirkt das selbstverständlich – aber wie wird aus einem physikalischen Phänomen (Wärme, Bewegung) eine messbare Zahl, mit der ein Computer arbeiten kann?
Diese Frage führt uns zur nächsten Ebene: der technischen Umsetzung. In den folgenden Kapiteln schauen wir uns an:
- Datenerfassung – Wie werden Daten aus der physikalischen Welt gewonnen? (Sensoren, Messgeräte, A/D-Wandler)
- Datenverarbeitung – Wie arbeiten Computer intern mit Daten? (Binärsystem, Zahlensysteme)
- Datenspeicherung – Wie werden Daten dauerhaft gesichert? (RAM, SSD, HDD, Datenbanken)
Diese drei Schritte bilden den Lebenszyklus von Daten – von der Erfassung über die Verarbeitung bis zur Speicherung und späteren Analyse.
Zusammenfassung 📌
- Daten sind Rohinformationen, die erst durch Kontext zu Information und Wissen werden.
- Big Data erweitert klassische Daten um neue Dimensionen: Menge, Geschwindigkeit und Vielfalt.
- Es gibt viele Arten von Daten - von Tabellen bis zu Videos.
- Attribute beschreiben Objekte; ihr Typ entscheidet, welche Analysen sinnvoll sind.
- Daten allein sind wertlos – entscheidend ist ihre Struktur und Nutzung.
- Daten zu verstehen ist der erste Schritt jeder Analyse.
- Attribute können qualitativ oder quantitativ sein.
- Je nach Skalenniveau (nominal, ordinal, intervall-, verhältnisskaliert) sind unterschiedliche Operationen erlaubt.
- Der korrekte Umgang mit Attributtypen verhindert Fehlinterpretationen in Analysen.
Im nächsten Kapitel beginnen wir mit der Datenerfassung und werden dabei eine faszinierende Parallele entdecken: Die Art, wie Computer Daten erfassen, ähnelt verblüffend der Art, wie wir Menschen unsere Umwelt wahrnehmen – durch Sensoren, Signalverarbeitung und intelligente Filterung.